Dos prisioneros se encuentran encerrados en celdas separadas acusados de algún delito. Ambos van a ser interrogados por separado por sus carceleros. Cada uno va a ser preguntado por la culpabilidad del otro. Cada preso puede optar por "Colaborar" con el otro, asegurando que el compañero se encuentra injustificadamente en la cárcel, o "Defraudar" acusándole.
Índice
Una versión muy sencilla Supongamos un conjunto de individuos; cada uno de los cuales posee una determinada cantidad de dinero. Cada persona puede decidir si invertir ese dinero en un cierto negocio, y en el caso de hacerlo, qué cantidad invertir. El negocio en cuestión es tan fabuloso que duplica inmediatamente cualquier inversión, pero con la peculiaridad de que el total del dinero resultante (el doble del dinero invertido) es repartido por igual entre todos los individuos, independientemente de la cantidad invertida por cada uno. Veamos algunos casos. Por ejemplo, si existen 10 individuos y todos invierten un euro, la inversión de 10 € producirá otros 10 € de beneficio y el resultado de 20 € será repartido entre todos, con lo que cada individuo obtendrá 2 € ¡Todos salen ganando! Si de los 10 individuos nadie invierte, no hay beneficio ni pérdida, y las finanzas de todos se mantienen como estaban. Pero si sólo uno de ellos invierte un euro, el euro se multiplica por dos y estos dos euros serán repartidas entre los 10, y ahora todos tendrán 1,2 € excepto el desprevenido inversor que tendrá 0,2 €. Si de los 10 individuos, sólo 5 de ellos invierten el euro, el resultado de 10 € es repartido entre los 10, de forma que los que no invirtieron ganarán un euro y los que invirtieron se quedarán como estaban al principio. 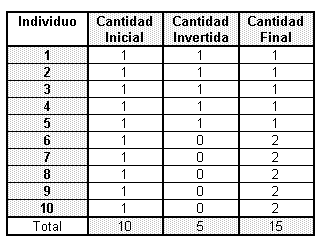
Obligatoriamente, cada individuo desconoce las inversiones que harán el resto de individuos. El objetivo de cada individuo es obtener el máximo beneficio posible, pero se encuentra entonces con un gran dilema: Si espera que los demás realicen pocas o incluso ninguna inversión, lo más adecuado es no invertir, ya que aunque el dinero se doble, al repartirse se obtendría mucho menos de lo que se tenía al principio. Pero si confía en la bondad de sus compañeros, y supone que estos realizarán grandes inversiones, ocurre lo mismo: la forma de obtener los máximos beneficios es invertir la mínima cantidad posible. Cada uno sabe que los demás serán capaces de llegar a la misma conclusión. Si eso ocurre y todos invierten la mínima cantidad, el beneficio será el mínimo para todos, y el negocio tan fabuloso que teníamos no estará siendo de utilidad para nadie. Por tanto, lo más inteligente parece colaborar, e invertir todos la máxima cantidad, para obtener todos el máximo beneficio. Pero, ¿puede uno confiar en que los demás también lo harán? En conclusión, lo razonable para obtener el máximo beneficio es no invertir absolutamente nada. Pero si todos siguen este razonamiento, ese beneficio máximo será cero. En cambio, si todos los individuos evitan su capacidad para la lógica, por ejemplo, realizando inversiones aleatorias (supongamos que con una distribución de probabilidad uniforme dentro del rango de las posibles inversiones), casi con toda seguridad, la cantidad de dinero aumentaría constantemente, tanto para todo el grupo como para individuos aislados. Podemos identificar las acciones orientadas hacia el beneficio propio como "racionales". Este es un ejemplo en el que la cooperación corresponde con un acto irracional que sin embargo, cuando ésta es la forma de actuar de un número suficiente de individuos, produce al grupo y a los individuos muchísimos más beneficios que el egoísmo racional. [ Volver al Indice ]
Algunos dilemas en la vida real Se puede pensar que la duplicación del dinero del caso anterior no tiene paralelismo en la vida real. No existen en los mercados de valores inversiones que dupliquen su valor inmediatamente. Sin embargo, sí existe una mercancía que se devuelve multiplicada, en muchos casos a todos por igual, a partir de la suma de aportaciones individuales. Esa mercancía es el conocimiento en centros de documentación públicos y libres como Internet. El conocimiento es el "dinero" que las personas pueden "invertir" y obtener multiplicado. Una persona puede plasmar en un documento conocimientos que le ha costado meses descubrir. Otra persona podrá en tan solo unas horas aprender sobre ese tema. Bastará con leer el documento. Pero no sólo eso. La utilidad de la suma del conocimiento de unos y otros será superior a la suma de las utilidades de los conocimientos independientes. La utilidad del todo es mayor que la utilidad de la suma de las partes. Otro dilema relacionado con el conocimiento es el que se produce en un imaginario equipo de desarrollo de software en el que algunos puestos de trabajo tal vez desaparezcan si el proyecto fracasa. Los programadores pueden optar por ocultar su conocimiento al resto, con la intención de destacar y asegurar su permanencia en la empresa. Pero si todos se comportasen de esta forma empezarían los problemas: tareas que se repiten innecesariamente, errores cometidos una y otra vez, el proyecto puede convertirse en un caos y tal vez nadie conserve su puesto. Si todos compartiesen todo su conocimiento, el proyecto tendría más probabilidades de éxito, y sería más probable que se mantuvieran todos los puestos de trabajo. Pero si uno comparte su conocimiento, ¿se podrá confiar en que los demás también lo harán? Podemos pensar que en general sí, ya que los equipos de trabajo en los que la cooperación sea baja tendrán menos probabilidades de éxito y por tanto más de desaparecer. Si ingresamos en un equipo de trabajo, es probable que el equipo coopere entre sí. ¿O tal vez no? Supongamos que el objetivo de cada individuo es no perder el propio puesto de trabajo. Hay dos estrategias razonables: no compartir el conocimiento y tratar de que sea otro el expulsado, o compartirlo y tratar de que ninguno lo sea. Pero si el equipo es grande, la influencia del propio trabajo sobre el éxito total puede ser baja. Si nadie coopera ¿por qué cooperar? Y si todos cooperan ¿por qué cooperar? Pero si todos siguen este razonamiento tal vez todos resulten perjudicados. [ Volver al Indice ]
El dilema del prisionero Veamos el siguiente caso. Dos prisioneros se encuentran encerrados en celdas separadas acusados de algún delito. Ambos van a ser interrogados por separado por sus carceleros. Cada uno va a ser preguntado por la culpabilidad del otro. Cada preso puede optar por "Colaborar" con el otro, asegurando que el compañero se encuentra injustificadamente en la cárcel, o "Defraudar" acusándole. Existen por tanto cuatro posibilidades, que ninguno defraude, que lo hagan los dos, que lo haga el primero o el segundo. |
Si... | ...entonces | | el jugador 1... | y el jugador 2... | el jugador 1 recibe... | y el jugador 2 recibe... | | Coopera | Coopera | 3 | 3 | | Coopera | Defrauda | 0 | 5 | | Defrauda | Coopera | 5 | 0 | | Defrauda | Defrauda | 0 | 0 |
Cada prisionero recibe un premio en función de esta tabla, mayor cuanto mayor es el número que aparece a la derecha. El 0 puede significar una pena de cárcel, el 3 la libertad; y el 5 la libertad y una indemnización. Supongamos que somos el jugador 2. Si el jugador 1 defrauda, es indiferente lo que hagamos, ya que recibiremos el castigo. Pero si el jugador 1 coopera con nosotros, el premio recibido es mayor si nosotros a su vez le defraudamos a él. En resumen, haga lo que haga el jugador 1, para el jugador 2 lo mejor es defraudar. Y lo mismo ocurre para el jugador 1: haga lo que haga el jugador 2, lo mejor es defraudar. Ya que las decisiones son independientes, y dado que el objetivo de cada uno es lograr el máximo beneficio personal, lo racional es defraudar. Pero si los dos se comportan racionalmente, ambos recibirán el castigo. [ Volver al Indice ]
Gramática: Formato de las reglas Esta es la gramática en BNF (Forma de Backus-Naur, estilo Yacc). En rojo aparecen algunos comentarios.
Un jugador se compone de reglas
jugador : "BEGIN PLAYER"
"NAME="
IDENTIFICADOR
reglas
"END PLAYER"
;
Puede haber una o más reglas
reglas : regla
| regla
reglas
;
Una regla tiene la forma: "SI condiciones ENTONCES conclusion", y puede tener además una prioridad
regla : "BEGIN RULE"
listaCondiciones
accion
"END RULE"
| "BEGIN RULE"
prioridad
listaCondiciones
accion
"END RULE"
;
A cada regla se le puede asignar una prioridad para que en el caso de poder dispararse mas de una regla, se ejecute la regla de prioridad mas alta.
prioridad : "PRIORITY="
NUMERO
;
listaCondiciones: "CONDITION="
condiciones
;
Puede haber una o más condiciones separadas por AND, o puede no haber condición y la regla ser cierta siempre
condiciones : condicion
| condicion
"AND"
condiciones
;
condicion : cond_el
| cond_yo
| cond_np
| "ALWAYS"
| tantoPorCiento
;
cond_el : "HE HAS"
jugada
"IN NP="
partida
;
cond_yo : "I HAVE"
jugada
"IN NP="
partida
;
cond_np : "NP="
partida
| "NP=MULTIPLE OF"
NUMERO
;
partida : NUMERO
| "PA-"
NUMERO
;
accion : "ACTION="
jugada
| "ACTION="
jugada
"(" tantoPorCiento ")"
;
jugada : "COOPERATE"
| "DEFRAUD"
;
tantoPorCiento : NUMERO
"%"
;
[0-9]+ { return NUMERO; }
[A-Za-z0-9\_\-]+ { return IDENTIFICADOR; } [ Volver al Indice ]
Ejemplo 1: siempre cooperar
Se trata de cooperar siempre
BEGIN PLAYER
NAME=jugador_ejemplo_1
BEGIN RULE
CONDITION=ALWAYS
ACTION=COOPERATE
END RULE
END PLAYER
|
Los espacios y tabuladores son opcionales, se ignoran. NAME puede ser cualquier combinación de numeros, letras y los simbolos "_" y "-", sin espacios. Otra forma de hacer lo mismo es:
BEGIN PLAYER
NAME=jugador_ejemplo_1
BEGIN RULE
PRIORITY=0
CONDITION=ALWAYS
ACTION=COOPERATE
END RULE
END PLAYER
|
A cada regla se le puede asignar una prioridad. La prioridad es útil cuando existen varias reglas, y es posible que la condición sea cierta para más de una regla. En ese caso se ejecutará la regla de prioridad más alta (con el número más alto). Si se diera el caso de que la prioridad más alta la tiene más de una regla del conjunto de las que pueden dispararse, entonces el programa elegirá una al azar. [ Volver al Indice ]
Ejemplo 2: siempre defraudar Se trata de defraudar siempre
BEGIN PLAYER
NAME=jugador_ejemplo_2
BEGIN RULE
CONDITION=ALWAYS
ACTION=DEFRAUD
END RULE
END PLAYER
|
Si se cumple la condición (es ALWAYS y por tanto siempre se cumple), entonces se defrauda
Otra forma de hacer lo mismo es:
BEGIN PLAYER
NAME=jugador_ejemplo_2
BEGIN RULE
CONDITION=ALWAYS
ACTION=DEFRAUD(100%)
END RULE
END PLAYER
|
Si se cumple la condición (es ALWAYS y por tanto siempre se cumple), entonces se realizan acciones al azar de forma que se defrauda el 100% de las veces
Otra forma de hacer lo mismo es:
BEGIN PLAYER
NAME=jugador_ejemplo_2
BEGIN RULE
CONDITION=ALWAYS
ACTION=COOPERATE(0%)
END RULE
END PLAYER
|
Si se cumple la condición (es ALWAYS y por tanto siempre se cumple), entonces se coopera el 0% de las veces, es decir, se defrauda siempre. [ Volver al Indice ]
Ejemplo 3: cooperar y defraudar alternativos Se trata de cooperar y defraudar alternativamente
BEGIN PLAYER
NAME=jugador_ejemplo_3
BEGIN RULE
PRIORITY=2
CONDITION=NP=MULTIPLE OF 2
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=1
CONDITION=ALWAYS
ACTION=DEFRAUD
END RULE
END PLAYER
|
La primera regla tiene mayor prioridad que la segunda Si el número de partida es multiplo de 2 (partidas pares), se coopera El resto de los casos, se defrauda [ Volver al Indice ]
Ejemplo 4: cooperar el 47% de las veces Se trata de cooperar el 47% de las veces y defraudar el resto
BEGIN PLAYER
NAME=jugador_ejemplo_4
BEGIN RULE
CONDITION=ALWAYS
ACTION=COOPERATE(47%)
END RULE
END PLAYER
|
La regla se cumple siempre, y consiste en cooperar 47 veces de cada cien. Para ello se genera un numero al azar de 1 a 100. Si el numero es menor o igual que 47, se coopera y en caso contrario, se defrauda.
Otra forma de hacer lo mismo es:
BEGIN PLAYER
NAME=jugador_ejemplo_4
BEGIN RULE
PRIORITY=2
CONDITION=47%
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=1
CONDITION=ALWAYS
ACTION=COOPERATE
END RULE
END PLAYER
|
La primera regla tiene mayor prioridad que la segunda. Para saber si se cumple la condición de la primera regla, se genera un número al azar de 1 a 100. Si el numero es menor o igual que 47, entonces la condición se cumple y se ejecuta la acción, que es defraudar. Si no se cumple, entonces se analiza la otra regla, que siempre se cumple y por tanto se coopera. [ Volver al Indice ]
Ejemplo 5: Donde las dan las toman Se trata de cooperar la primera vez, y repetir la última jugada de nuestro contrincante el resto de las partidas.
BEGIN PLAYER
NAME=jugador_ejemplo_5
BEGIN RULE
PRIORITY=2
CONDITION=NP=1
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=1
CONDITION=HE HAS COOPERATE IN NP=PA-1
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=1
CONDITION=HE HAS DEFRAUD IN NP=PA-1
ACTION=DEFRAUD
END RULE
END PLAYER
|
Si la partida es la primera, se coopera. Si el contrario ("HE") ha cooperado en la partida anterior, es decir, en numero de partida igual a la partida actual menos uno ("NP=PA-1"), entonces se coopera Si el contrario ("HE") ha defraudado en la partida anterior, es decir, en numero de partida igual a la partida actual menos uno ("NP=PA-1"), entonces se defrauda [ Volver al Indice ]
Ejemplo 6: Mezcla de cooperador y toma y daca Se trata de cooperar la primera vez, y el resto de las partidas se hace: el 40% de las veces se coopera, y el 60% restante, se coopera solo si nuestro contrincante ha cooperado en sus dos ultimas partidas.
BEGIN PLAYER
NAME=jugador_ejemplo_6
BEGIN RULE
PRIORITY=4
CONDITION=NP=1
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=3
CONDITION=40%
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS COOPERATE IN NP=PA-1
AND HE HAS COOPERATE IN NP=PA-2
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=1
CONDITION=ALWAYS
ACTION=DEFRAUD
END RULE
END PLAYER
|
Regla 1: Si la partida es la primera, se coopera. Regla 2: Se genera un número al azar de 1 a 100. Si el numero es menor o igual que 40, entonces la condición se cumple y se ejecuta la acción, que es cooperar. Si no se cumple, entonces se analizan las reglas 3 y 4. Regla 3: Si el contrario ("EL") ha cooperado en la partida anterior, es decir, en numero de partida igual a la partida actual menos uno ("NP=PA-1"), y en la anterior a esta ("NP=PA-2"), entonces se coopera Regla 4: Si no se ha cumplido ninguna de las anteriores, se defrauda [ Volver al Indice ]
Ejemplo 7: Rencoroso Total Se trata de cooperar la primera vez y todas las siguientes (suponemos que son 10) mientras el otro también lo haga. Si alguna vez el contrario defrauda, entonces desde ese momento se defrauda siempre.
BEGIN PLAYER
NAME=RENCOROSOTOTAL
BEGIN RULE
PRIORITY=3
CONDITION=NP=1
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=1
CONDITION=ALWAYS
ACTION=COOPERATE
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-1
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-2
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-3
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-4
ACTION=DEFRAUD
END RULE
BEGIN RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-5
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-6
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-7
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-8
ACTION=DEFRAUD
END RULE
BEGIN RULE
PRIORITY=2
CONDITION=HE HAS DEFRAUD IN NP=PA-9
ACTION=DEFRAUD
END RULE
END PLAYER
|
[ Volver al Indice ]
Bibliografía - Poundstone, William. El dilema del prisionero. Alianza Editorial. 1992.
- Bass, Thomas A. y Martín, Luna. "Por qué ganan los buenos". Revista Muy Interesante, nº 203. Abril 1998.
- Axelrod, Robert "La evolución de la cooperación" Alianza Universidad. 1996.
- Hofstadter, Douglas R. "Temas Metamágicos". Revista Investigación y ciencia. Agosto 1983.
- Dawkins, Richard. El gen egoísta. Salvat Ciencia. 1994.
- Kropotkin, Peter Alexeivich. El apoyo mutuo. Ediciones Madre Terra. 1970.
Sobre el autor
|
Manuel de la Herrán nació en Bilbao en 1971. Es ingeniero informático y ha trabajado en varias empresas desarrollando tecnología en Internet y dirigiendo sus departamentos técnicos (Okté, Cocotero, EnLaPrensa). Ha escrito un libro en forma de ensayo, así como numerosos artículos sobre Evolución, Computación Evolutiva, Algoritmos Genéticos, Inteligencia Artificial, Datamining y Datawarehouse, OLAP y Bases de Datos Multidimensionales, Bases de datos Oracle y Programación en Internet. Ha sido profesor de la Universidad de Deusto y ha participado en la creación de proyectos como IIEH, Gaia (finalista iBest 2000), y REDcientífica (Premio Nacional Sociedad de la Información).
|
© Copyright 2001-2004 Manuel de la Herrán Gascón.
© Copyright 2001-2004 REDcientífica.
Todos los derechos reservados.
[Evaluar este artículo]
|